Gaussian Analytic Functions


A Poisson point process (left) and zeros of a planar Gaussian analytic function.
Description:
The random power series

where an are independent standard complex Gaussian random variables is a planar Gaussian analytic function. It is shown in [3] that the distribution of the zeros of fC(z) are invariant under translations in the plane, so it is natural to compare the distribution of zeros to a Poisson point process with the same intensity (see above). The function

where an are again independent standard complex Gaussian random variables is a hyperbolic Gaussian analytic function. All its zeros lie within the unit disk, and once this region is identified with the hyperbolic plane, the distribution of zeros is invariant under symmetries of the hyperbolic plane [3]. We prove in [1] that the zeros of fU form a determinantal processwith the Bergman kernel:
 .
.
Moreover, the set of moduli
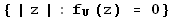
has the same law as the set {Uk1/2k}, where Uk are i.i.d. random variables uniform on [0,1].
Dynamics:
One may consider a dynamic version of the zero set by computing the zeros of the function

where an(t) are i.i.d. Ornstein-Uhlenbeck processes. In other words,

where {Wn}are independent complex Brownian motions. Click here to see a movie.
References:
-
Zeros of the i.i.d. Gaussian power series: a conformally invariant determinantal process. (Y. Peres and B. Virág). Acta Math. To appear.
-
Zeros of Gaussian analytic functions. (M. Sodin). Math. Res. Lett., 7(4): 371–381.
-
Random complex zeros, I. Asymptotic normality. (M. Sodin and B. Tsirelson). Preprint. (2003).