Here are two riddles, the solutions of which I will discuss next week. Interested readers are welcome to email me solutions.
Thanos Problem
Thanos, the all-powerful supervillain, can snap his fingers and destroy half of all the beings in the universe.
Suppose now there are ![]() Thanoses, each snapping his fingers in a sequence, one after the other. When a Thanos snaps his finger, each being (Thanos or human) dies independently with probability
Thanoses, each snapping his fingers in a sequence, one after the other. When a Thanos snaps his finger, each being (Thanos or human) dies independently with probability ![]() .
.
Question: Out of ![]() people on Earth, how many can we expect to still be alive at the end? More formally, let
people on Earth, how many can we expect to still be alive at the end? More formally, let ![]() be the probability that a human being survives. Initial values:
be the probability that a human being survives. Initial values: ![]() ,
, ![]() .
.
Show that
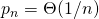 , that is,
, that is, 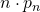 is bounded between positive constants.
is bounded between positive constants.Does
 converge? If so, to what limit?
converge? If so, to what limit?Does
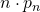 converge? If so, to what limit?
converge? If so, to what limit?

Note: this problem was posted (with fewer details) by Oliver Roederon on the 538 blog, but without an analytical solution. The plot is due to Laurent Lessard (github).
Particles Problem
Suppose there are ![]() particles in the unit square. Initially one particle is awake and all others are sleeping. Each awake particle moves in the unit square at speed
particles in the unit square. Initially one particle is awake and all others are sleeping. Each awake particle moves in the unit square at speed ![]() in a direction you prescribe and wakes up any sleeping particle it encounters. The particles that are awake move simultaneously and particles can change direction at any point in time.
in a direction you prescribe and wakes up any sleeping particle it encounters. The particles that are awake move simultaneously and particles can change direction at any point in time.
Question: Show that you can wake up all the particles by time ![]() . Note: I learned this problem from Maria Gringlaz.
. Note: I learned this problem from Maria Gringlaz.
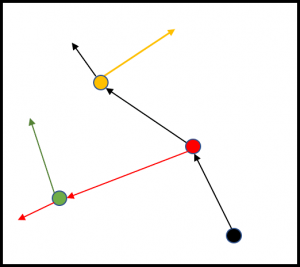
New: A solution to the particles problem is now available here.
2 thoughts on “Thanos and Particles Riddles”